4. 다층 퍼셉트론 및 딥러닝 기초
신경망이란
- 기계학습 역사에서 가장 오래된 기계학습모델.
- 1950년대 퍼셉트론 -> 1980년대 다층퍼셉트론
- 사람의 뉴런
- 두뇌의 가장 작은 정보처리 단위
- 세포체는 간단한 연산, 수상돌기는 신호 수신, 축삭은 처리 결과를 전송
- 사람은 10^11개 정도의 뉴련을 가지며, 뉴런은 1000개 가량 다른 뉴련과 연결되어 있어 10^14개 정도의 연결
신경망의 종류
<신경망 모델>
- 전방 신경망과 순환 신경망
- 얕은 신경망과 깊은 신경망
- 결정론 신경망과 스토캐스틱 신경망
* 결정론 신경망 : 확률적으로 랜덤하게 바뀌지 x
스토캐스틱 신경망 : 확률적으로 바뀜
퍼셉트론이란
- 퍼셉트론은 노드, 가중치, 층과 같은 새로운 개념을 도입하고 학습 알고리즘을 창안,
- 퍼셉트론은 원시적 신경망이지만, 딥러닝을 포함한 현대 신경망은 퍼셉트론을 병렬과 순차 구조로 결합하여 만듦 => 현대 신경망의 중요한 구성 요소
퍼셉트론의 구조
- 입력측과 출력층을 가짐
- 입력층은 연산을 하지 않으므로 퍼셉트론은 단일 층 구조
- { 입력층의 i번째 노드 } == { 특징벡터 x = (x1,x2,x3,...,xd)의 요소 xi를 담당 }
- 바이어스 노드 x0은 항상 1 => 입력값과 가중치를 모두 곱한 다음 바이어스(편향)을 더함
- 출력층은 한개의 노드
- i번째 입력층 노드와 출력층을 연결하는 에지는 가중치 wi를 가짐
퍼셉트론의 동작
동작 순서
- 특징값과 가중치를 곱한 결과를 모두 더하여 s 구함
- s를 활성함수에 적용함
- 활성함수로 계단함수를 사용하므로 최종 출력 y는 +1 또는 -1
결정직선

- 특징공간에 존재하는 특징벡터를 분류하여 특징공간을 분리할 수 있는 결정직선 d(x)
- 결정직선은 전체 공간을 +1과 -1의 두 부분공간으로 분할하는 분류기 역할
- 2차원은 결정직선, 3차원은 결정 평면, 4차원 이상은 결정 초평면
퍼셉트론의 학습
- 목적함수 설계

- 그레디언트 계산

- 행렬을 사용하면 위의 식을 간결하게 표기할 수 있다.!

다층퍼셉트론
퍼셉트론의 한계 = 선형분류기
==> 민스키의 [Percenptrons]
- 다층 구조를 이용한 극복방안 제시
- 1974년 오류 역전파 알고리즘 제안
- 1986년 다층 퍼셉크론 이론 정립 => 신경망 부활
다층 퍼셉트론의 핵심 아이디어
- 은닉층
- 원래 특징공간을 분류하는 데 유리한 새로운 특징 공간으로 변환
- 시그모이드 활성함수
- 퍼셉트론은 계단함수를 활성함수로 사용 => Hard Decision
- 다층 퍼셉트론은 시그모이드를 활성함수로 사용 => Soft Decision
- soft decision은 출력이 연속값인데, 출력을 신뢰도로 간주함으로써 더 융통성 있게 의사결정 가능
- 오류 역전파 알고리즘
- 다층 퍼셉트론은 여러 층이 순타적으로 이어진 구조
- 역방향으로 진행하면서 한 번에 한 층씩 그레디언트를 계산하고 가중치를 갱신하는 방식의 오류 역전파 알고리즘을 사용.
특징 공간 변환


==> hidden layer(은닉층)가 입력된 데이터들이 특징공간을 유리하게 변환해줌.
==> 은닉층을 지난 후 활성함수까지 지나야 퍼셉트론 실행 완료!
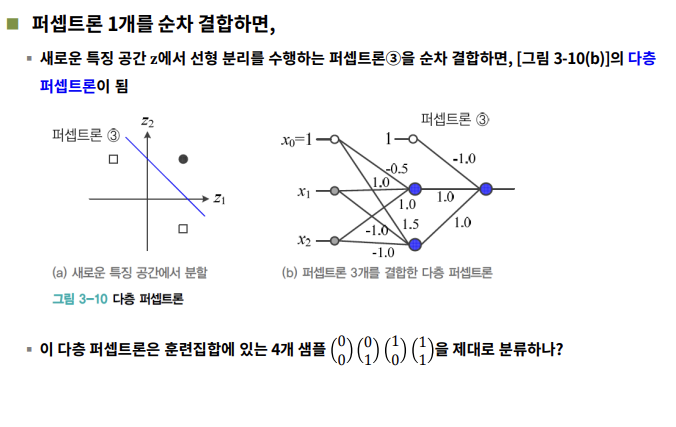
==> 유리하게 변환된 특징공간을 분리하는 퍼셉트론(3)을 순차결합하면 다층퍼셉트론 완성!!~!
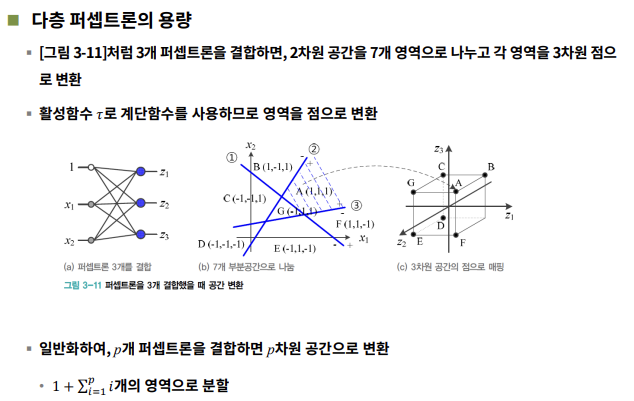
- 일반화 : p개의 퍼셉트론을 결합하면 p차원 공간으로 변환
활성함수
딱딱한 의사결정 vs 부드러운 의사결정
- 딱딱한 의사결정
- 영역을 점으로 변환
- 계단함수
- 부드러운 의사결정
- 영역을 영역으로 변환
- 나머지 활성함수=> 로지스틱 시그모이드, 하이퍼볼릭 탄젠트 시그모이드
다양한 활성함수

- 퍼셉트론은 계단함수
- 다층 퍼셉트론은 로지스틱 시그모이드와 파이퍼볼릭 탄젠트
- 딥러닝은 ReLU를 사용
다층 퍼셉트론 구조
- 입력층 - 은닉층 - 출력층 (2층 구조)
- d+1개의 입력노드 (d는 특징의 개수). c개의 출력 노드(c는 부류 개수)
- p개의 출력 노드 : p는 하이퍼 매개변수(사용자가 정해주는 매개변수)
- p가 너무 크면 과잉적합, 너무 작으면 과소적합

- 가중치 = 다층 퍼셉트론의 매개변수

- 다층 퍼셉트론은 특징 벡터x를 출력 벡터 o로 매핑하는 함수로 간주할 수 있다~


- 노드가 수행하는 연산

- 은닉층1의 가중치 벡터값과 특징벡터를 곱한 값 zsum을 활성함수에 넣음
- 이 값을 은닉층2의 가중치 벡터값과 특징벡터를 곱한 값 osum을 활성함수에 넣어 출력 노드 연산

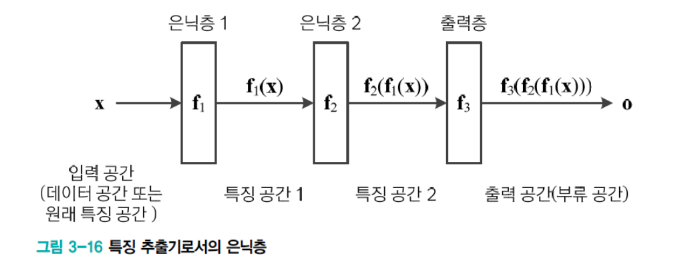
- 은닉층 = 특징 추출기
- 은닉층은 특징 벡터를 분류에 더 유리한 새로운 특징 공간으로 변환
- feature learning(특징학습)이라 부름
오류 역전파를 위한 목적함수의 정의
훈련집합
- 특징 벡터 집합 X = {x1,x2,x3,..,xn}과 부류 벡터 집합 Y = {y1,y2,y3,...,yn}
- 부류 벡터는 원핫 코드로 표현됨!!
* One-Hot Encoding : 단어 집합의 크기를 벡터의 차원으로 하고, 표현하고 싶은 단어의 인덱스에 1의 값을 부여하고, 다른 인덱스에는 0을 부여하는 단어의 벡터 표현 방식
기계학습의 목표 "Y = f(X)"
==> 모든 샘플(특징벡터)을 옳게 분류하는 함수 f를 찾는 일
목적 함수
- 평균 제곱 오차 MSE(Mean Squared Error) 정의
다층퍼셉트론 동작
- 다층 퍼셉트론은 특징벡터 x를 출력벡터 o로 매핑하는 함수로 간주할 수 있다.
- 은닉층은 특징 추출기
- 은닉층은 특징벡터를 분류에 더 유리한 새로운 특징공간으로 변환 "feature learning"
오류 역전파를 위한 목적함수의 정의
- 훈련집합
- 특징벡터 집합 X + 부류벡터 집합 Y
- 부류벡터의 특징벡터는 원핫코드로 표현됨
==> 기계학습은 모든 샘플을 옳게 분류하는 함수 f(=모델)를 찾아야 한다.
- 목적함수
- 평균제곱오차(MSE mean squared error)로 정의됨
이 뒷장은 오류 역전파 알고리즘을 설계하는 방식으로
은닉층이 2개인 다층퍼셉트론을 예로 들어 설계하고 있다.
목적함수 J를 U1과 U2로 미분한 값으로 빼 오류 역전파를 설계한다.
오류역전파 유도식을 모두 정리해보면 최종적으로

위의 그림과 같이 정리된다.
오류 역전파 알고리즘은 위의 식을 이용하여
출력층의 오류를 역방향(왼쪽)을 전파하며 그레디언트를 계산하는 알고리즘이다.
다층퍼셉트론의 특성
- 모든 함수를 정확하게 근사할 수 있는 능력
- 은닉층을 하나만 가지더라도 은닉 노드가 충분히 많다면 원하는 정확도만큼 근사화할 수 있다.
- 하지만 은닉노드를 충분히 갖는 것은 불가능하다.
- 오류 역전파 알고리즘의 빠른 속도
- 전방계산보다 1.5~2배정도의 시간이 걸리며 비교적 빠르게 계산하는 것을 확인할 수 있다.
- 성능 향상을 위한 휴리스틱의 중요성
- 데이터 희소성, 잡음, 비숙한 신경망의 구조 때문에 순수한 최적화 알고리즘으로는 높은 성능이 불가능하다.
- 따라서 성능 향상을 위해 갖가지 휴리스틱을 개발하고 공유해야한다
- 휴리스틱 개발에서 주요 쟁점
- 아키텍처
- 초기값
- 학습률
- 활성함수
요런 다층퍼셉트론임에도 불구하고
잡음섞인 상황에서 음성인식 성능이 저하되고, 필기주소 인식 능력이 떨어지고, 바둑에서의 한계를 보여줬다.
이때 한계를 극복하며 등장한 것이 딥러닝!!
딥러닝
딥러닝이란?
- 다층퍼셉트론에 은닉층을 여러개 추가하면 깊은 신경망이 된다.
- 딥러닝은 깊은 신경망을 학습시키는 알고리즘이다.
- 딥러닝은 새로운 응용을 창출하고 인공지능 제품의 성능을 획기적으로 향상시켰으며 현대 기계학습을 주도하고 있다.
딥러닝의 등장
- 배경
- 1980년대에 이미 깊은 신경망 아이디어은 등장했다.
- 하지만 실현이 불가능했다. 깊은 신경망은 학습이 불가능했는데 이는 아래의 이유때문이었다.
- 그레디언트 소멸 문제 => 학습 불가능
- 작은 훈련집합
- 과다한 계산 시간(값비싼 슈퍼 컴퓨터)
- 하지만 꾸준한 연구로 성장했다.
- 학습률에 따른 성능 변화 양상
- 모멘텀의 영향
- 은닉 노드 수에 따른 성능 변화
- 데이터 전처리의 영향
- 활성함수의 영향
- 규제 기법의 영향 등...
딥러닝의 기술 혁신 요인
- 컨볼루션 신경망이 딥러닝의 가능성을 엶
- 값싼 GPU 등장
- 인터넷 덕분에 학습 데이터가 크게 늘어남
- 계산은 단순한데 성능은 더 좋은 활성함수 => 요즘 ReLU
- 과잉 적합을 방지하는데 효과적인 다양한 규제 기법
- 층별 예비학습 기법 개발
특징 학습의 부각
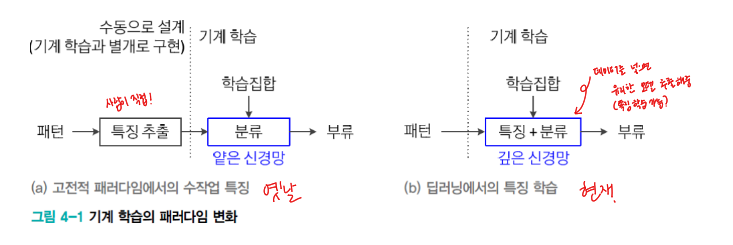
- 기계학습의 패러다임의 변화
- 고전적인 다층 퍼셉트론
- 은닉층은 특징 추출기
- 얕은 구조이므로 센서로 획득한 원래 패턴을 그대로 입력하면 낮은 성능을 보였다.
- 따라서 사라밍 수작업으로 특징을 구상하고 구현하여 신경망에 입력해야 했다.
- 현대 기계 학습(딥러닝)
- 특징 추출을 학습으로 설계 <= 특징 학습 feature learning
- 원래 패턴이 신경망의 입력 <= 통째 학습 end-to-end learning
- 고전적인 다층 퍼셉트론
- 특징 학습feature learning (or 표현 학습 representation learning)
- 앞단계 은닉층은 에지나 코너와 같은 저급 특징 추출
- 뒷단계 은닉층은 추상적인 형태의 고급 특징을 추출
- 특징 학습이 강력해짐에 따라
- 기존 응용에서 획기정인 성능 향상 ex. 영상인식, 음성인식, 언어번역 등
- 새로운 응용 창출
- 분류나 회귀뿐 아니라 생성모델이나 화소 수준의 영상 분할
- CNN과 LSTM의 협력모델 등이 가능해짐.
* 층이 많아졌기에
앞층에서는 사람들이 육안으로 알아볼 수 있는 저급 특징으로 추출하고
뒷 층에서는 사람이 알아보기 힘든 고급 특징을 추출하여 성능이 높아졌다.
이는 Convolution Layer의 특징이기도 하다.
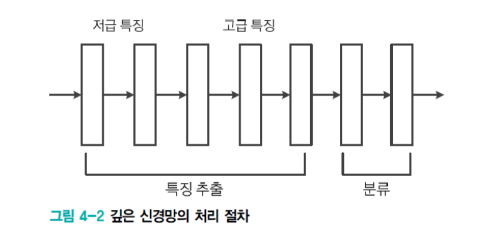
깊은 다층 퍼셉트론 구조와 동작
깊은 MLP(DMLP, deep MLP)의 구조
- 입력층(d+1개의 노드)과 출력층(c개의 노드)
- L-1개의 은닉층(입력층은 0번째 은닉층, 출력층은 L번째 은닉층으로 간주)



깊은 다층 퍼셉트론 학습
또 식을 정리해서 결국 일케 되는데

진짜 뭐라는지 모르겠다..
역사적 고찰
- 학습 알고리즘의 주요 개선

여기서 아까 등장했던 gradient 소멸 문제를 설명할 수 있다.
다층 퍼셉트론 때는 활성함수로 시그모이드 함수를 사용했었는데
시그모이드는 미분하면 값이 커질수록 기울기가 거의 0에 수렴한다.
따라서 gradient를 계속 곱하다 보면 너무 작아져 소멸 문제가 발생했었는데
깊은 다층 퍼셉트론에서는 ReLU를 사용하여 이를 극복했다.

- CNN의 부상(Convolution Neural Net)
- ex. MNIST 인식 경쟁 => CNN을 이용한 앙상블 모델에서 오류율이 0.23%로 최소로 나옴.
- ILSVRC 자연영상 인식 경쟁에서 CNN이 DMLP보다 확연시 우월함을 확인했다.